Tietotekniikan koulutusohjelma

Etusivu → ensimmäisen opintovuoden opinnot → perusopinnot → matematiikka 2A

Matematiikka 2A (6 op)

Sisältö

Polynomi: jaollisuus, jakoalgoritmi, tekijöihin jako nollakohtien avulla.

Epäyhtälöt: reaalilukujen järjestyksen ominaisuudet, polynomi- ja murtoepäyhtälöt.

Reaalifunktiot: alkeisfunktiot (potenssifunktio, polynomifunktio, trigonometriset funktiot, eksponentti- ja logaritmifunktiot) sekä niihin liittyvät yhtälöt, yhdistetty funktio, käänteisfunktio. Sovelluksia

Reaalifunktioiden differentiaalilaskenta: raja-arvo, jatkuvuus, derivaatta, derivoimissäännöt alkeisfunktioiden derivaatat. Sovelluksia.

Analyyttinen tasogeometria: suora, toisen asteen käyrät, suoran, ympyrän ja ellipsin parametriesitykset. Sovelluksia.

Edeltävät opinnot

Matematiikka 1A

Vaadittavat suoritukset

Välikokeilla ja kotitehtävillä.

Kirjallisuus

Launonen, E., Sorvali, E., & Toivanen, P. 1998. Teknisten ammattien matematiikka 3A, 3B ja 3C. Porvoo: WSOY.

Omat huomiot

Tahti oli kova, monet saivat hylätyn, emmekä silti ehtineet analyyttiseen tasogeometriaan.

Keskeisiä kaavoja

Trigonometrian kaavoja
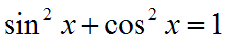
sin(x)²+cos(x)²=1
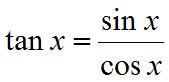
tan(x)=sin(x)/cos(x)
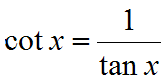
cotx=1/tan(x)
Palautuskaavat
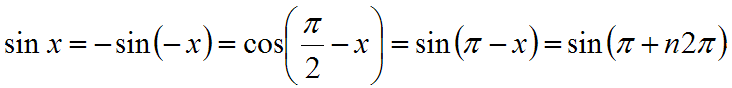
sin(x):n palautuskaava
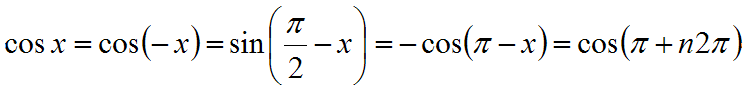
cos(x):n palautuskaava
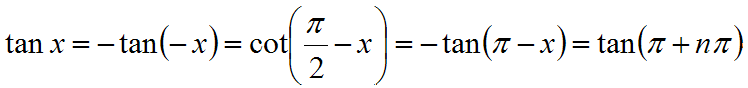
tan(x):n palautuskaava
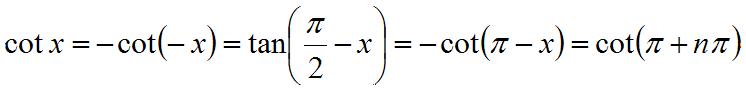
cot(x):n palautuskaava
Summakaavat
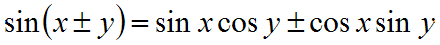
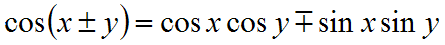
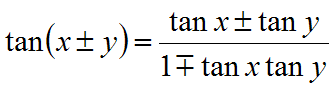
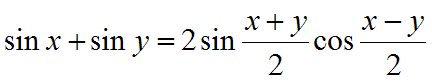
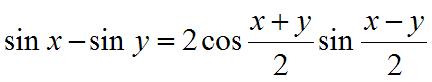
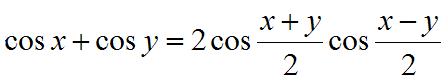
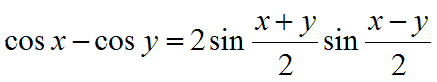
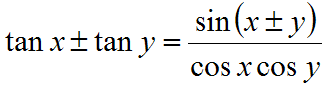
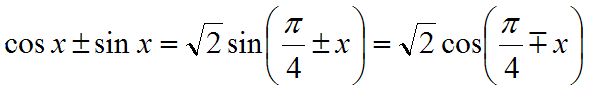
kaava
kaava
kaava
kaava
kaava
kaava
kaava
kaava
kaava
Derivointisääntöjä
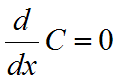
Derivaatta vakiosta on yhtä suuri kuin 0.
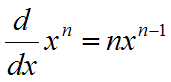
Derivaatta x:n n:stä potenssista on yhtä suuri kuin nx^(n-1).
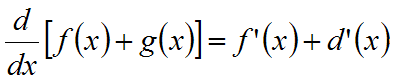
Funktioiden summan derivaatta on yhtkä suuri kuin kummankin funktion derivaatan summa.
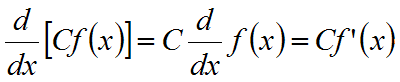
Funktion ja vakion tulon derivaatta on yhtä suuri kuin funkion derivaatta kerrottuna vakiolla.
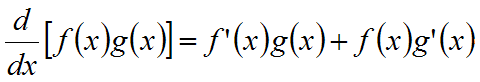
Tulon derivaatta
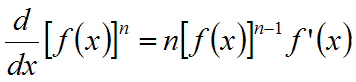
Potenssin derivaatta
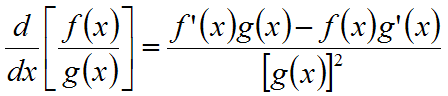
Osamäärän derivaatta


Harri Paavola, harri@artturi.org

Edellisen päivityksen ajankohta: 4.4.2006.

Get Firefox